Matematik Ders Notları: ORAN-ORANTI SORU ÇÖZÜM TAKTİKLERİ

a/b = c/d gibi iki oranın eşitliğine orantı denir.

Doğru Orantı:Sayılardan biri artarken diğeride artıyorsa doğru orantılı demektir.Mesela reel sayılarda çıkarma ve bölme doğru orantılıdır.

Ters Orantı:Sayılardan biri artarken diğeri azalıyorsa ters orantılı demektir.Mesela reel sayılarda çarpma ve toplama ters orantılıdır.

NOT:Bir soruda mesela 2 ve 3 ile orantılı diyorsa doğru orantılı olarak alıcağız.

ÖRN:26 sayısını 2 ve 3 ile doğru 5 ile ters orantılı şekilde parçalayalım.

         2.k  ,3.k,k/5 şeklinde yazarız.2k+3k+(k/5)=26
                                                         26k/5=26
                                                         k=5
     2.5=10     3.5=15    5/5=1

Bileşik Orantı

ÖRN:18 İşçi 12 gün çalışarak 120 dönümlük tarlayı çapıyor.
       Aynı nitelikte 14 işçi 140 dönümlük tarlayı kaç günde çapalayabilir?

Cevap:18 işçi 12 gün çalışıyorsa 1 tanesinin 18.12 gün çalışması gerekir.Yani 1 işçi 216 gün çalışarak 120 dönümlük tarlayı çapalar

               1 işçi 216 gün çalışarak 120 dönümlük araziyi çapalarsa    1 gün çalışarak 120/216 dönümlük araziyi çapalar.Yani   1 işçi 1 gün çalışarak 5/9 dönümlük araziyi çapalar.

          1 işçi 1 günde 5/9 lu araziyi çapalarsa 140 dönümlük araziyi   140/(5:9) günde çapalar.Yani 252 günde çapalar.
         1 işçi 252 günde 140 dönümlük araziyi çaparlarsa   14 işçi 252/14'ten 18 günde çapalar.

(BU TARZ SORULARDA EZBERLEMEYİN.EZBERLERSENİZ UNUTMA OLASILIĞINIZ YÜKSEK BİR SORU TARZI ÇÜNKÜ BU)

ARİTMETİK ORTALAMA

Verilen sayı dizisindeki terimlerin toplamının, terim sayısına bölünmesiyle elde edilen değerdir.
a+b+c+d+,,,,,,+z
------------------
n

GEOMETRİK ORTALAMA

$G={\sqrt[ {n}]{x_{1}\cdot x_{2}\dotsb x_{n}}}$

HARMONİK ORTALAMA

$H={\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}$

İki veri için harmonik ortalama

Yalnız iki tane veri, (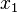 $x_{1}$ ve $x_{2}$ ) elde bulunursa, bunlar için harmonik ortalama H şöyle ifade edilebilir.

$H={\frac {{2}{x_{1}}{x_{2}}}{{x_{1}}+{x_{2}}}}.$

Bu halde bulunan harmonik ortalama, bu iki sayının aritmetik ortalamasına şöyle ilişkilidir;

$A={\frac {{x_{1}}+{x_{2}}}{2}},$

ve bu iki verinin geometrik ortalamasi olan G ise

$G={\sqrt {{x_{1}}\cdot {x_{2}}}},$

Bu harmonik ortalamaya şöyle ilişkilidir:

$H={\frac {G^{2}}{A}}.$

Böylece

$G={\sqrt {{A}{H}}}$ ,

olur. Bu demektir ki geometrik ortalama, aritmetik ortalama ve harmonik ortalama'nın geometrik ortalaması olur.
Ama çok dikkat edilmelidir ki bu sonuç yalnız ve yalnız iki veri için geçerli olur.

Matematik Ders Notları

Sayfalar

10 Şubat 2014 Pazartesi

ORAN-ORANTI SORU ÇÖZÜM TAKTİKLERİ

İki veri için harmonik ortalama

Hiç yorum yok:

Yorum Gönder